KıZıL - TeBeSiR - Mutlak Değer

MUTLAK DEĞER

Matematikte, mutlak değer bir gerçel sayının işaretsiz değerini verir. Örneğin, 3; hem 3'ün hem de -3'ün mutlak değeridir. Bilgisayarlarda ise, bu fonksiyonu ifade etmek için kullanılan matematiksel fonksiyon genelde abs(...)'dir (Örnek: abs(sayi) gibi.)

Mutlak değer fonksiyonunun gerçel sayılarla kullanımı dışında, geniş bir matematiksel kullanım alanı vardır. Örneğin, mutlak değer karmaşık sayılar gibi kümeler için de tanımlanabilir.Kısacası mutlak değer; bir sayının 0'a olan uzaklığıdır

Karmaşık sayılara kadar olan kısımda, verilen mutlak değer özellikleri karmaşık sayılar kümesine aynen uygulanamaz. Önerme 1'i ele alırsak:

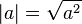
$|a| = sqrt{a^2}$

her gerçel sayının bir karmaşık sayı olduğunu ve,

bir karmaşık sayının

$z = x + iy,$

olduğunu düşünürsek göreceğiz ki, gerçel sayılarda y katsayısı 0'a eşit. Öyleyse gerçekte $z$ 'nin mutlak değer (ya da karmaşık sayılarda bazen modül olarak adlandırılır) şu şekilde tanımlanabilir.

Öyleyse bir gerçel sayıda bu işlemi şöyle gerçekleştirebiliriz:

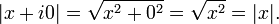
$|x + i0| = sqrt{x^2 + 0^2} = sqrt{x^2} = |x|.$

Mutlak değer bir sayının orijine uzaklığını verir. Karmaşık sayılar iki boyutlu düzlem üzerinde incelendiğinden Pisagor teoremi iki nokta arasındaki uzaklığı bulmada işimize yarayacaktır.Karmaşık düzlemde iki karmaşık sayı arasındaki uzunluğu bulmak içinse aynı gerçel sayılardaki

$z = x + mathrm{i}y = r (cos phi + mathrm{i}sin phi ) ,$

ise, ve

$bar{z} = x - iy$

z karmaşık sayısının eşlenik'i ise, açıkça görülür ki:

$|z| = r,$

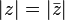$|z|=|bar{z}|$